Frequency Space and the Fourier Transform

When we hear sound (= compressed air) or observe radiation (= a bunch of photons), we do this in the spatial domain, the normal 3d world. But would'nt it be nice to see which frequencies (for sound) or which wavelengths (inverse frequency, for photons) there are? This would be called the frequency domain, where we don't care where the sound/photons came from or where it goes, but rather which components are in there.

In this article, I outline how the frequency domain works, and how we get from spatial to frequency domain (and back), using the so-called Fourier transform.

Disclaimer: This article is just a subset of Fourier analysis, and there are a lot of omissions, e.g. just handling sound in air. The aim is to get a feel for the topic and for the mathematics.

1 Sound

Let's start with why we would want the frequency domain in the first place. Here we will take sound because we are more familiar with it, but it works for all waves including light and electric signals. Imagine still air, and a loudspeaker membrane. You start vibrating it once per second, also called 1 Hz. The vibration compresses the air and produces a so-called longitudinal wave (the other kind of compression wave is transverse, but not important for now). We have produced a clear tone with a frequency f=1 Hz, and the size of the wave on the acoustic membrane determines the loudness or amplitude A=10 (-5..+5 in the rightmost image below).


Longitudinal wave by Wikipedia	Loudspeaker membrane by Pixabay	Acoustic membrane by Wikipedia

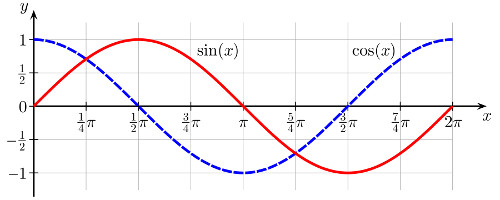
You will notice that the membrane swings in a non-linear manner, being faster in the middle and slowest at its peaks. Turns out that it describes a sine wave (or cosine wave), which is very nice for us because trigonometric functions have been mathematically researched for like forever and we have a lot of tools to work with. In the image below, you see the amplitude A=2 on the y axis (-1..+1), and the x axis shows not the time (I would have expected 1s for f=1 Hz) but rather some trigonometric angle 0..2π (which is like 0..360°, but in radian). For now, assume that an angle of 2π is equal to 1 second; then we have our pure sound wave, with amplitude over time.

Sine and cosine wave by Wikipedia

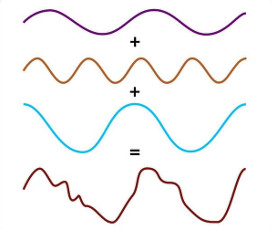
Now in the real world, almost every sound we hear isn't a pure sound but rather a combination of all kind of frequencies and amplitudes (same goes for most light we see, the noisy current in electric wire, and so on). Below in the left image, we add something like f=2 Hz, 4 Hz and 1 Hz (with A=1, 1, and 2 or so) to arrive at a wave that looks kind of chaotic.


Wave addition by Christine Daniloff, MIT		Square wave addition by LucasVB via Nautilus

Turns out that the inverse also works: Any wave can be built by adding multiple sine waves together! Though some, like the square wave in the right image above, need infinitely many components. Which brings us to the question: How do we best formulate that?

2 Frequency Domain

The answer lies in the frequency domain. Where before in the time domain, you had amplitude A on the y axis and time t (or angle φ) on the x axis, now in the frequency domain, you still have A on the y axis but now the frequency f on the x axis.

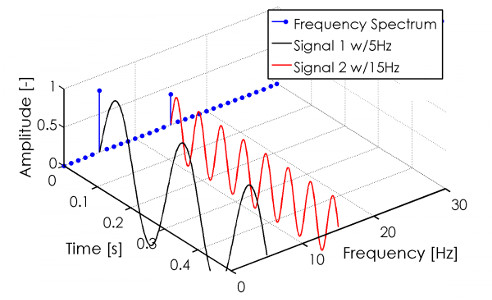Time vs. frequency domain by Paul Balzer

The surprising part is that there is no notion of time in the frequency domain: That is why it only works for repeating waves like sound. If you have a non-repeating wave, you need to split it into smaller parts that are repeating, e.g. the single tones of a trumpet within a song. In the graph above, we can't hear anything since human hearing goes from 20..20000 Hz only, but it would be some tone (5 Hz) and the same tone two octaves higher (*3, landing at 15 Hz).

Other nice things we can do in the frequency domain is to increase bass by amplifying the lower 5 Hz tone, increase treble by amplifying the 15 Hz tone, make the sound richer by adding 10 Hz (*2), 20 Hz (*4), 25 Hz (*5) and so on, or put in some distortion by adding some other frequencies around the other tones. Unsurprisingly, musicians do that a lot.

But back to that math side of life. In the time domain, we have a wave function s(t)=A for a certain timespan which, given a time t, gives us the amplitude A. Any periodic function is fine, but we need to know its period (duration) T. Then we can represent s(t) as an addition of frequency bands, a so-called Fourier series:

Whoa, that is a lot, so easy here. Given the time t, we want the amplitude A, which is a sum over some frequencies f from zero to infinity (step size=1). For each of those f, we have a cosine and a sine, both of which are multiplied with the so-called Fourier coefficients A_f and B_f, which exist once per frequency f and determine how strongly a frequency counts within the summation.

Next, what's inside the cos/sin? Whatever it is, we want to map it to 0..2π, because that is the working range of cos/sin. First, the 2π indicates that whatever follows should be in the 0..1 range, and the t/T (time point within the total duration) does just that. And finally, higher frequencies f must map to larger ranges, e.g. for f=2 Hz, the term inside cos/sin maps to 0..4π which ensures that the complete sine wave is run through twice.


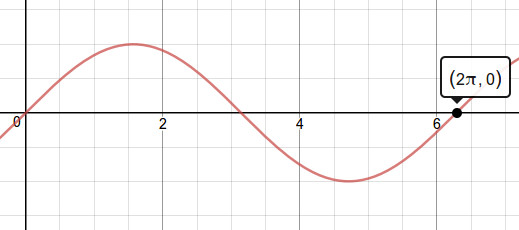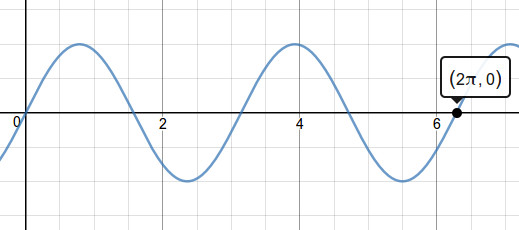sin(1x) for f=1Hz, wave run through once, via Desmos calculator		sin(2x) for f=2Hz, wave run through twice

So why cosine and sine? Ok, so the formula above isn't really the original one, just the more useful, that's why I showed it to you first. The reason is that the start of the sum does not necessarily begin at 0, but rather some phase shift φ_f, which can be in the range 0..2π and is different for each frequency f. With that, the formula reads:

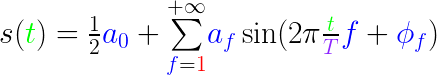
Ok, one by one. The most important thing is at the end, inside the sine: We have an ugly addition of the previous term and φ_f, which complicates the math. Second, the sum runs from 1 to infinity, not 0 to infinity, because we cannot deactivate the sine by setting f=0 anymore, and must add it (or rather, half of it) in front.

In order to get rid of the +φ_f within the sine, we use the trigonometric identity sin(a+b)=cos(a)*cos(b) + sin(a)*sin(b), then define A_f=a_f*sin(φ_f) and B_f=a_f*cos(φ_f), and voila, we are back in our first representation.

A tiny side note: You might have asked yourself why the summation of f=1, 2, 3, ... with a step size 1 leads to terms cos(2π), cos(4π), cos(6π), ... and the same with sines. After all, should'nt we also be able to count in steps of 0.5 Hz, or 2 Hz? Turns out that these terms are basis functions (i.e. orthogonal) to each other, much like how in 3d space the basis functions [1 0 0]^T, [0 1 0]^T and [0 0 1]^T are orthogonal, meaning that in a vector [x y z]^T, each of the three components only influences one basis function (=axis) and does not mess with the others. Think:

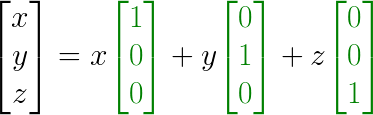
With basis functions in dark green. And now let it sink in that in the frequency domain, the basis functions are cos(2π), sin(2π), cos(4π), sin(4π), cos(6π), sin(6π), ... instead. Whew. Ok, done? Then back to the Fourier series.

To summarize: We have to know the global period T and use a time variable t which runs from 0..T. Per frequency f, we use (so far unknown) coefficients A_f and B_f, which include the local amplitude a_f and the phase shift φ_f. Now we just need to determine the frequency domain function ŝ(f)=[A_f, B_f] (read: s-cap) which gives us the per-frequency coefficients. So how do we get those?

3 Fourier Transform

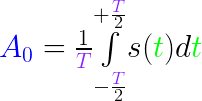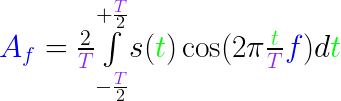${\color{Blue} A_0}=\frac{1}{{\color{Purple} T}} \underset{-\frac{{\color{Purple} T}}{2}}{\overset{+\frac{{\color{Purple} T}}{2}}{\int}} s({\color{Green} t}) d{\color{Green} t}$		${\color{Blue} A_f}=\frac{2}{{\color{Purple} T}} \underset{-\frac{{\color{Purple} T}}{2}}{\overset{+\frac{{\color{Purple} T}}{2}}{\int}} s({\color{Green} t}) \cos(2\pi\frac{{\color{Green} t}}{{\color{Purple} T}} {\color{Blue} f}) d{\color{Green} t}$
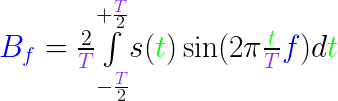${\color{Blue} B_0}=0$		${\color{Blue} B_f}=\frac{2}{{\color{Purple} T}} \underset{-\frac{{\color{Purple} T}}{2}}{\overset{+\frac{{\color{Purple} T}}{2}}{\int}} s({\color{Green} t}) \sin(2\pi\frac{{\color{Green} t}}{{\color{Purple} T}} {\color{Blue} f}) d{\color{Green} t}$
A₀ and B₀ and ...		A_f and B_f in the frequency domain

Deducing the above formulas is rather elaborate, so let's develop some intuition, starting with A_f. Within the integral, assume tiny slices (essentially a sum) where we take the exact cosine function that we used in the Fourier series in the previous section, and multiply each slice with the original s(t) value at that slice position. In essence, A_f represents how much of s(t) falls within the cosine of the frequency f. Afterwards, we normalize it by the size of T (factor 2 because cos(x)=-1..+1 has y range 2).

B_f is analogous, just with sin. A₀ can be seen as constant "base level", and as such has no sine/cosine and also normalizes without an additional factor 2. B₀ is not needed since we do not need two base levels.

And that would be almost all I can give you in terms of intuition, except there is an even more elegant formulation of the Fourier series and transform.

4 Complex Fourier Transform

Which is the complex variant. A complex number is basically a 2-vector [real part, imaginary part] which is written a+bi, where i is sort of like the y axis [0 1]^T, and there is a strange rule i²=-1. The reason why that is relevant for us is that Eulers formula says e^ix=cos(x)+i*sin(x).

A simpler way to express a sum of cosine and sine? Color me intrigued. Unfortunately I do not have the slightest intuition for the complex fourier transform.

Conclusion